Прості виду 4k+1

Ми приведемо тут класичний доказ того, що кожне просте виду 4k+1 подано як сума двох квадратів; цей доказ належить, по суті, Ейлерові. Він складається з двох кроків. Перший крок полягає у встановленні того, що деяке кратне подано у виді; на другому кроці ми встановимо, що уявно у виді .

Перший крок еквівалентний доказу вирішення рівняння.

для будь-якого простого виду 4k+1. Ми вже знаємо, що це так, з критерію Ейлера для квадратичних вирахувань і невирахувань.

Другий крок доказу починається із вже встановленого факту, з якого виходить, що існує таке натуральне m, для якого.

Ми можемо, звичайно, припускати, що z лежить між і (цього можна добитися, віднімаючи з r відповідне кратне р). Припустивши це, отримуємо.

Звідси, зокрема, витікає, що існують такі цілі х і 2/, для яких виконується рівність.

де m — натуральне число, менше. Покажемо тепер, що якщо m>1, то знайдеться таке натуральне, менше m, для якого рівняння все ще вирішується в цілих х і у. Звідси (якщо повторити це міркування кілька разів) слідуватиме, що вирішується рівняння, в якому m=1.

Міркування проводяться таким чином. Визначимо два цілі числа u і v, що лежать між і (включно, якщо m парне), які порівнюються відповідно з х і у по модулю m :

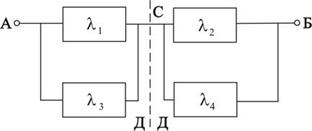
(3).

Тоді, так що (4).

для деякого цілого r. Помітимо, що r не може бути рівне 0, оскільки тоді u і v дорівнювали б 0, а тому х і у були б кратні m; а це суперечить рівності (2), бо звідси та із (2) витікає, що просте число ділиться на m. Число r задовольняє нерівності.

Перемножимо рівність (2) і (4), застосовуючи тотожність (1). Це дає.

Важливо відмітити, що кожне з чисел і ділиться на m. Дійсно, зважаючи на рівняння (3) i.

Отже, (5) можна розділити на m2, що дає з деякими цілими X і Y. Тим самим ми довели, що існує таке натуральне число r, менше m, для якого rp подано у вигляді суми двох квадратів.

Як ми вже говорили, цього вистачає, щоб довести представлення у вигляді суми двох квадратів. Проілюструємо цей доказ на чисельному прикладі. Візьмемо це просте виду 4k+1. Ми знаємо, що рівняння вирішуване і його рішення легко знайти підбором або за допомогою таблиці індексів. Число є рішенням цього рівняння:

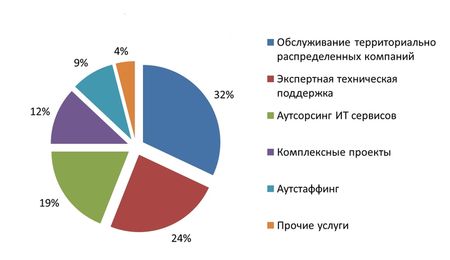
Початковим пунктом доказу, як і в загальному випадку, служить рівність. Наслідуючи план доказу, приводимо числа 60 і 1 по модулю 13; отримаємо числа -5 і 1.

Аналогом рівності (4) служить рівність.

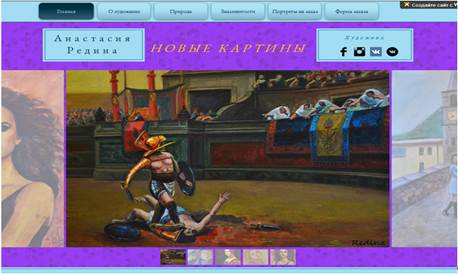
Наступний крок полягає в перемножуванні двох рівностей і застосуванні тотожності (1). Отримуємо.

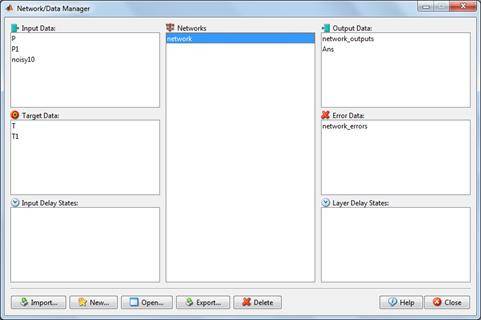
Числа справа, як це і повинно бути, діляться на 13, скорочення призводить до рівності.

Далі цей процес повторюється. Числа -23 і 5, приведені по модулю 2, дають 1, відповідне рівняння має вигляд.

Перемножуючи його з попередньою рівністю і застосовуючи тотожність (1), отримуємо.

І, нарешті.

У зв’язку з доведеною загальною теоремою треба помітити що представлення р у вигляді єдине (якщо виключити очевидні можливості заміни х і зміни їх знаків). Ферма, звернувши увагу на цей факт, назвав його «фундаментальною теоремою про прямокутні трикутники»: звідси витікає, що існує рівно один прямокутний трикутник, гіпотенуза якого рівна, а катети вимірюються натуральними числами.

Довести єдиність представлення не важко. Припустимо, що має місце рівність.

(6).

Ми знаємо, що рівняння має рівно два рішення:. Значить.

Оскільки знаки чисел х, у, X, Y несуттєві, можна вважати, що виконано.

Перемножимо рівність (6) і застосуємо тотожність (1). Тоді отримаємо.

Далі в силу (7). Значить, обидва числа справа діляться на р і рівність можна розділити на. Це дає представлення 1 у вигляді суми двох квадратів, а таке представлення єдине:. Таким чином, в попередній рівності одне з чисел xX+yY і xY — уХ має дорівнювати 0. Якщо хY — уХ = 0, то, оскільки х, у і X, Y взаємно прості, або х = X і у = Y, або х = -X і у = - Y. Аналогічно, якщо хХ + уУ = 0, то або х = Y і у= -X, або х = -Y і у =X. У кожному з цих випадків обидва представлення в (6), по суті, однакові.