Властивості функцій неперервних на компакті

Коли ми вивчали функції дійсної змінної, то ми бачили, що якщо функція неперервна на сегменті, то вона мала цілий ряд властивостей. Деякі з цих властивостей мають місце для функцій неперервних на компактах.

Нехай маємо метричні простори Х і У, через будемо позначити відстань в Х, — відстань в У; К Х компакт в Х.

Теорема 4.1. Якщо функція f неперервна на компакті К, то образ f (К), цього компакта, є компактом.

Доведення. Нехай f:K XY неперервна функція на компакті К. Через f (К) позначимо образ К при даному відрбраженні. Покажемо, що f (К) компакт. Нехай у₁, у₂,…, у_п послідовність з f (К). Через х_п позначимо — прообраз у_п. Якщо якась точка у_п має декілька прообразів, то будемо брати будь-який з них. Таким чином ми отримали послідовність {х_п}, х_п є К. Так як К компакт, то з {х_п} можна виділити підпослідовність, яка збігається до точки, яка належить К. Нехай, f (х₀)=у₀f (K). Розглянемо підпослідовність послідовності {у_п}. Поскільки f неперервна в х₀, то. Звідси й слідує, що К є компактом.

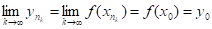
Нехай Е Х, f: ЕУ. f (Е), образ Е при даному відображенні. Якщо виявиться, що для кожного у є f (Е) існує тільки одне х є Е таке, що f (х)=у, то на f (Е) можна визначити функцію, яка кожному уf (Е) ставить у відповідність хЕ таке, що f (x)=y. Ця функція називається оберненою до f. Позначають обернену функцію: . Зрозуміло, що областю визначення оберненої функції є f (E), а областю значень — Е. При цьому f є оберненою до .

Очевидно, для того, щоб функція f мала обернену, тобто була оборотною, необхідно і достатньо, щоб відображення f:Ef (E) — було взаємно-однозначним.

Теорема 4.2. Якщо функція f:KXY, неперервна на компакті і відображення f:Kf (K) — взаємно-однозначне, то обернене відображення — неперервне на f (K).

Доведення. Доведення проведемо методом від супротивного. Припустимо, що не є неперервною функцією на f (K). Тоді існує y₀f (K) таке, що в ній має розрив. Нехай f ^-1(y₀)=х₀. Оскільки f ^-1 має розрив в точці у₀, то існує >0 таке, що для кожного натурального п, знайдеться у_пf (K) таке, що, але. Нехай х_п=f ^-1(у_п), х_пК. Так, як К компакт, то з послідовності {x_n} можна виділити підпослідовність, яка збігається до точки із множини К,, з нерівності слідує.

.

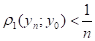
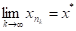
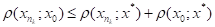
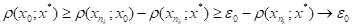
коли. Звідси робимо висновок, що х₀х^*. Внаслідок неперервності f маємо.

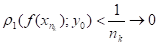
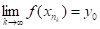
(f(x^*)y₀, так як у₀=f (x₀), а відображення взаємно-однозначне). З іншого боку, коли, тобто, що суперечить (4.1). Теорему доведено.

Теорема 4.3. Якщо функція f:KXY, неперервна на компакті К, то вона і рівномірно неперервна на К.

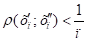
Доведення. Доведення проведемо методом від супротивного. Припустимо, що функція f не є рівномірно неперервною на К. Тоді існує ₀>0 таке, що для кожного натурального п знайдуться точки, які належать множині К такі, що, але .

Одержали дві послідовності. Поскільки К — компакт, то з можна виділити підпослідовність, яка збігається до точки х₀, яка належить К. Розглянемо підпослідовність послідовності. З нерівності слідує, що. Так, як функція f неперервна в точці х₀, то і. Тобто.

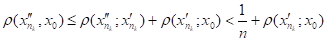
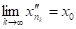
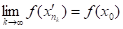
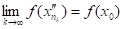
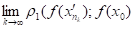
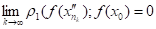
= (4.3).

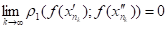
З нерівності робимо висновок, що, що суперечить нерівності при всіх натуральних k. Теорему доведено.

Розглянемо деякі властивості функцій неперервних на компакті, значення яких є дійсні числа, тобто f:KXR (R — множина дійсних чисел). Такі функції називаються числовими.

Теорема 4.4. (Вейєрштрасса) Якщо числова функція неперервна на компакті КХ, то вона обмежена на К і приймає на ньому найбільше та найменше значення.

Доведення. Нехай f:KXR є неперервною на К. Внаслідок Т.4.1, множина f (K) — компакт, а, оскільки, компакт є обмеженою множиною, то f (K) є обмеженою множиною.

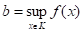
Доведемо, що функція приймає найбільше і найменше значення на К, тобто існують точки х₁ і х₂ такі, що для всіх хК виконується нерівність:. Нехай. Візьмемо >0. Тоді існує хК таке, що. Звідси робимо висновок, що b є точкою дотику f (K). Внаслідок замкненості f (K) (Т. 1.1), bf (K). Значить існує х₁К, що f (x₁)=b.

Аналогічно показуємо, що існує х₂К таке, що f (x₂)=а, де. Теорема доведена.