Теорема Банаха. 
Теоретичні основи для реалізації розділу "Елементи функціонального аналізу та диференціальне числення функцій багатьох змінних" курсу математичного аналізу за допомогою комп’ютерних технологій

Одним із важливих прикладів неперервних відображень є, так звані, стискуючі відображення.

Означення 3.1. Нехай f відображення метричного простору X₁ в X₂. Відображення називається стискуючим, якщо: 0<<1: x, yX₁, справедлива нерівність: .

Легко показати, що стискуюче відображення є неперервним. Дійсно, нехай х₀Х₁. Тоді. Якщо хх₀, то, а значить. Отже, відображення є неперервним.

Дуже часто в математиці виникає потреба з’ясувати при яких умовах те чи інше рівняння має на деякій множині єдиний розв’язок. При розв’язуванні цієї задачі використовують властивості стискуючих відображень заданих в повних метричних просторах.

Означення 3.2. Нехай f відображає Х в Х. Точка х₀Х, називається нерухомою точкою оператора f, якщо f (x₀)=x₀.

Теорема (Банаха). Якщо f:XX є стискуючим відображенням, і Х повний метричний простір, то відображення f в даному просторі має єдину нерухому точку.

Доведення. Візьмемо довільне х₀Х, х₁=f (x₀), x₂=f (x₁)_,…x_n=f (x_n-1),… В результаті одержали послідовність {x_n}X. Тоді.

(3.1).

Візьмемо будь-яке п, тоді p

(^n+p-1+^n+p-2+… …+ⁿ)(x₁;x₀)<(ⁿ+ⁿ⁺¹+…+^n+p-1+^n+p+…)(x₁;x₀)= (x₁;x₀).

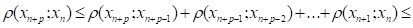
Оскільки 0<<1, то останній вираз при п, прямує до нуля так, що >0, n₀: nn₀, справедлива .

З останніх двох нерівностей одержуємо, що послідовність {x_n} є фундаментальною, а оскільки простір повний, то і збіжною до деякої точки аХ.

Внаслідок неперервності відображення f маємо:

.

Звідси слідує, що а є нерухомою точкою цього відображення.

Для доведення єдиності точки а, припустимо, що b є ще одна нерухома точка відображення: b=f (b), причому ab. Тоді матимемо:

бо 0<<1.

Прийшли до суперечності. Теорему доведено.